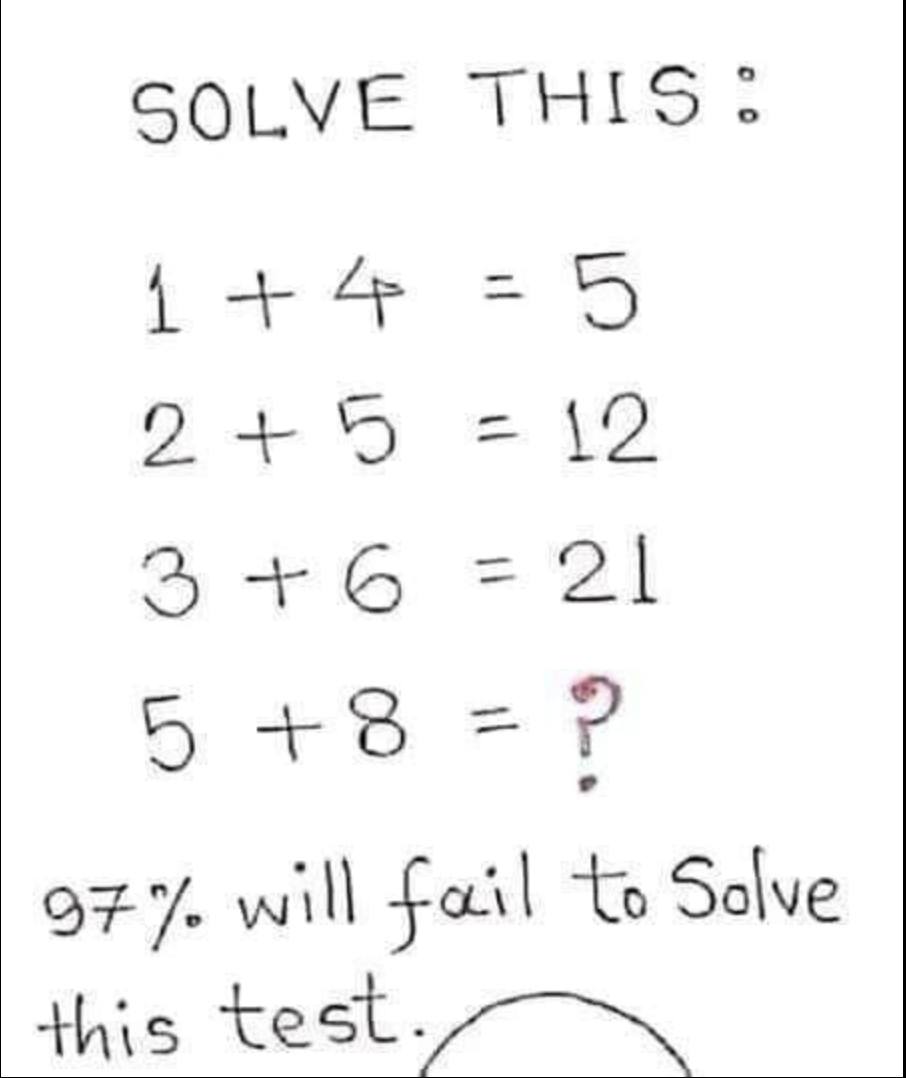What’s fascinating is that the chaos isn’t really about the numbers. It’s about interpretation.
Most viral math problems exploit a quiet weakness in how people remember math rules. We were taught procedures—“do multiplication before addition,” “work left to right,” “follow the order of operations”—but many of us never internalized *why* those rules exist or how strictly they apply. Over time, the rules blur together into intuition. And intuition, it turns out, varies wildly from person to person.
The internet, being the internet, turns that assumption into a battleground.
What’s especially interesting is how confident people are—even when they’re wrong. Or rather, even when there *is* no universally agreed-upon answer because the problem itself is ambiguous. Confidence online isn’t earned through correctness; it’s earned through certainty. The more sure you sound, the more likes you get.
And math problems are perfect fuel for this dynamic. Math carries cultural authority. There’s a sense that there *must* be a single correct answer, and that getting it right says something about your intelligence. So people aren’t just defending a number—they’re defending their competence.
That’s why these threads get so heated. Being wrong about a movie opinion is harmless. Being wrong about math feels personal.
But step back for a moment, and the situation becomes almost funny. Grown adults arguing over whether the answer is 1, 9, or 16. Entire comment sections reduced to repeating the same explanations louder and louder, as if volume might substitute for clarity.
Meanwhile, the original poster sits back and watches the engagement roll in.
Because that’s the other truth about viral math problems: they’re engagement machines.
They don’t need to be hard. They don’t even need to be fair. They just need to be slightly confusing and emotionally activating. Confusion creates comments. Disagreement creates shares. Outrage creates virality.
And yet, people keep falling for it.
Part of the appeal is nostalgia. These problems transport people back to school, to a time when answers felt concrete and testable. Solving it feels like reclaiming a piece of competence, a reminder that you “still got it.” Posting your answer is a small performance of intelligence in a public space.
Another part is community. Arguing in the comments is oddly bonding. Strangers align into temporary camps—Team 8 versus Team 2—each convinced they’re fighting for mathematical truth. It’s low-stakes conflict with just enough intellectual flavor to feel productive.
But there’s also something deeper going on.
These problems expose how differently people think. Some read equations visually. Others hear them as sentences. Some rely strictly on formal rules. Others lean on mental shortcuts. When those approaches collide, it feels like someone else is breaking the rules—even when they’re just following a different internal logic.
In that sense, the confusion isn’t a failure of intelligence. It’s a mismatch of assumptions.
Of course, eventually someone shows up with a clean, textbook explanation. They reference the order of operations. They rewrite the problem clearly. They explain why one answer is correct *if* the problem is interpreted a certain way. Sometimes they’re right. Sometimes they’re just the most persuasive.
The argument has taken on a life of its own. People aren’t looking for resolution; they’re looking for validation. Admitting ambiguity feels like losing. Saying “this problem is unclear” feels unsatisfying compared to declaring victory with a bold number and a smug emoji.
And so the debate continues, long after the math itself has stopped being the point.
What’s ironic is that real math—the kind mathematicians actually do—is full of nuance, precision, and careful definitions. Ambiguity is treated as a flaw to be fixed, not a weapon to be wielded. Viral math problems flip that on its head. They thrive on vagueness. They succeed by being just unclear enough to spark chaos.
In a way, these problems are less about math and more about the internet’s relationship with knowledge.
We like the idea of objective truth, but we love the drama of disagreement. We claim to value correctness, but we reward confidence and speed. We say we want to learn, but we rarely slow down long enough to question our assumptions.
So a simple equation becomes a mirror. It reflects how we argue, how we assert expertise, how uncomfortable we are with uncertainty.
Maybe that’s why these problems keep going viral. Not because they’re clever, but because they tap into something human.
The desire to be right.
The fear of being wrong.
The thrill of proving someone else wrong in public.
In the end, the internet never fully agrees. The post fades from your feed, replaced by a new problem, a new argument, a new set of confident answers. The cycle repeats.
And somewhere, someone is still typing, “It’s basic math,” completely unaware that *basic* is exactly where things get complicated.
So the next time a math problem leaves the internet scratching its head, it might be worth pausing before jumping into the comments. Not to calculate faster or argue harder—but to notice what’s really happening.
Because the most revealing part of the problem usually isn’t the answer.
It’s how desperately we want there to be one.